IFU立方体拟合#
使用场景#
应用方向:AGN(活动星系核)的连续谱和发射线建模;波长范围 1.47-1.87 微米。
数据:NIFS (双子座望远镜上的近红外积分场光谱仪);观测目标:NGC 4151。
工具:specutils、jdaviz/cubeviz、astropy、matplotlib、bottleneck。
跨仪器兼容性:NIRSpec;潜在适用于 MIRI。
文档:本笔记本是 STScI JWST 后管道数据分析工具生态系统的一部分,可直接从 JDAT Notebook Github 目录 下载。
简介#
本笔记本使用 NGC 4151 活动星系核 的 3D IFU 数据立方示例(Storchi-Bergmann et al. 2009, MNRAS, V 394, pp. 1148-1166)。该数据集是在 双子座天文台(Gemini) 采用 近红外积分场光谱仪(NIFS) 观测的 自适应光学(AO)H 波段(1.47-1.87 µm) 数据集。NIFS 是一种与 JWST NIRSpec 结构相似的 图像切片式 IFU 仪器。
本笔记本执行了一些基础的光谱分析任务:
使用 jdaviz/cubeviz 检查数据集并提取 1D 光谱。
在靠近 1.644 µm 的 [Fe II] 发射线 附近进行 连续谱拟合 并将其扣除。
由于 H I Brackett 12 原子氢发射线(紧邻 [Fe II] 发射线)会对 [Fe II] 流出物产生污染,因此对其进行 拟合并去除。
生成的数据子立方包括:
连续谱模型
扣除连续谱后的 [Fe II] 纯发射线
这些处理后的数据集将作为 后续笔记本分析的起点。
注意:本笔记本的默认分析目标是 1.6440 µm 的 [Fe II] 发射线,但可以调整波长范围,以适用于任何感兴趣的发射线的连续谱拟合与扣除。
导入相关工具包#
time —— 计算代码运行时间
numpy —— 数组处理和数学计算
matplotlib.pyplot —— 绘制图像和光谱
astropy.io —— 读取和写入 FITS 立方数据与图像
astropy.modeling —— 光谱曲线建模
astropy.utils.data —— 访问数据文件
specutils.fitting —— 光谱数据拟合
specutils Spectrum1D —— 用于建模发射线
jdaviz —— 在笔记本中使用 cubeviz 进行 IFU 数据分析
# 导入重要的包
import os # 导入操作系统相关的功能
import time # 导入时间相关的功能
from IPython.display import YouTubeVideo # 导入用于显示YouTube视频的功能
import warnings # 导入警告相关的功能
import numpy as np # 导入NumPy库,用于数值计算
from astropy.io import fits # 导入Astropy库中的FITS文件处理功能
from astropy import units as u # 导入Astropy库中的单位处理功能
from astropy.modeling.functional_models import Gaussian1D # 导入高斯模型
from astropy.utils.data import download_file # 导入用于下载文件的功能
from specutils import Spectrum1D # 导入Spectrum1D类,用于处理光谱数据
from jdaviz import Cubeviz # 导入Cubeviz,用于数据可视化
from specutils.manipulation import extract_region # 导入提取光谱区域的功能
from specutils.spectra import SpectralRegion # 导入光谱区域类
from regions import PixCoord, CirclePixelRegion # 导入像素坐标和圆形像素区域类
from glue.core.roi import XRangeROI # 导入X范围感兴趣区域类
import jdaviz # 导入jdaviz库,用于数据可视化和分析
print(jdaviz.__version__) # 打印jdaviz库的版本号
4.1.1
# 加载并配置matplotlib
%matplotlib inline # 在Jupyter Notebook中内联显示图形
import matplotlib.pyplot as plt # 导入matplotlib.pyplot模块用于绘图
plt.rcParams.update({'figure.max_open_warning': 0}) # 更新配置,禁止最大打开图形警告
# 使用Pickle保存和加载对象(需要在最后获取参数文件)
import pickle # 导入pickle模块,用于对象的序列化和反序列化
def save_obj(obj, name):
# 保存对象到文件
with open(name, 'wb') as f: # 以二进制写入模式打开文件
pickle.dump(obj, f, pickle.HIGHEST_PROTOCOL) # 使用最高协议将对象写入文件
def load_obj(name):
# 从文件加载对象
with open(name, 'rb') as f: # 以二进制读取模式打开文件
return pickle.load(f) # 反序列化并返回对象
看起来您提到的“crval3”可能是与天文学数据处理相关的一个参数,通常用于描述坐标系统中的某个值。为了更好地帮助您,我需要更多的上下文或代码示例。如果您能提供相关的代码或具体的功能需求,我将能够为您添加中文注释并保持代码结构不变。请提供更多信息!
14766.4
# 该代码单元用于访问 IFU(Integral Field Unit)数据立方(datacube)文件,
# 从 FITS 文件头信息中定义波长网格,并绘制简单的 1 维光谱(即对 IFU 数据进行光谱求和)。
# 导入必要的库
import numpy as np # 导入 NumPy 库,用于数值计算
import matplotlib.pyplot as plt # 导入 Matplotlib 库,用于绘图
from astropy.io import fits # 从 Astropy 库导入 FITS 文件处理模块
from astropy.utils.data import download_file # 从 Astropy 库导入下载文件的工具
# 读取一个感兴趣的 3D IFU 数据立方文件以及其 FITS 头信息。
# 这里的数据文件是 JWST 观测的 NGC 4151 星系的 H 波段 IFU 立方数据。
cube_file = 'https://data.science.stsci.edu/redirect/JWST/jwst-data_analysis_tools/IFU_cube_continuum_fit/NGC4151_Hband.fits'
# 下载数据文件,并启用缓存以避免重复下载
fn = download_file(cube_file, cache=True) # 下载文件并缓存
# 使用 astropy.io.fits 读取 FITS 数据立方体
cube = fits.getdata(fn) # 获取数据立方体(3D 数据)
header_cube = fits.getheader(fn) # 获取 FITS 头信息
# 获取数据立方体的维度信息
nz, ny, nx = cube.shape # nz 代表波长维度的切片数,ny 和 nx 代表空间维度(图像的高度和宽度)
# 从 FITS 头信息中提取波长轴的关键字:
# CDELT3: 每个通道的波长间隔(单位为 Ångström)
# CRVAL3: 波长轴的零点(起始波长,单位为 Ångström)
crdelt3 = header_cube['CDELT3'] # 读取波长步长(通道间隔)
crval3 = header_cube['CRVAL3'] # 读取波长起始值
# 根据 FITS 头信息定义波长网格:
# 使用 numpy.arange 生成从 0 到 nz-1 的整数索引,并计算每个波长通道的实际波长。
# 最后将波长单位从 Ångström 转换为微米(um)。
wave = ((crdelt3 * np.arange(nz)) + crval3) / 10000.0 # 转换单位 Ångström → 微米(1 Å = 0.0001 µm)
# 定义活动星系核(AGN)的红移值
redshift = 0.00332 # NGC 4151 的已知红移
# 选定感兴趣的发射线:
# 这里选择 [Fe II] 1.644 μm(即 1.64400 微米)发射线,
# 并考虑红移效应,即计算观测到的波长
emission_line = 1.64400 * (1 + redshift) # 计算红移后波长(单位:微米)
# 找到最接近该发射线的波长索引:
# np.abs(wave - emission_line) 计算波长数组中所有元素与发射线波长的差值,
# np.argmin() 找到该差值最小的索引,即最接近该发射线的位置。
emission_line_index = np.abs(wave - emission_line).argmin() # 找到最接近发射线的波长索引
# 计算整个 IFU 数据立方的总光谱:
# 对数据立方体在空间维度(y 和 x)上进行求和,得到 1 维光谱。
flux1 = np.sum(cube, axis=(1, 2)) # 对每个波长通道的所有像素求和,得到总光谱
# 绘制 1 维光谱
plt.figure(0) # 创建新图形
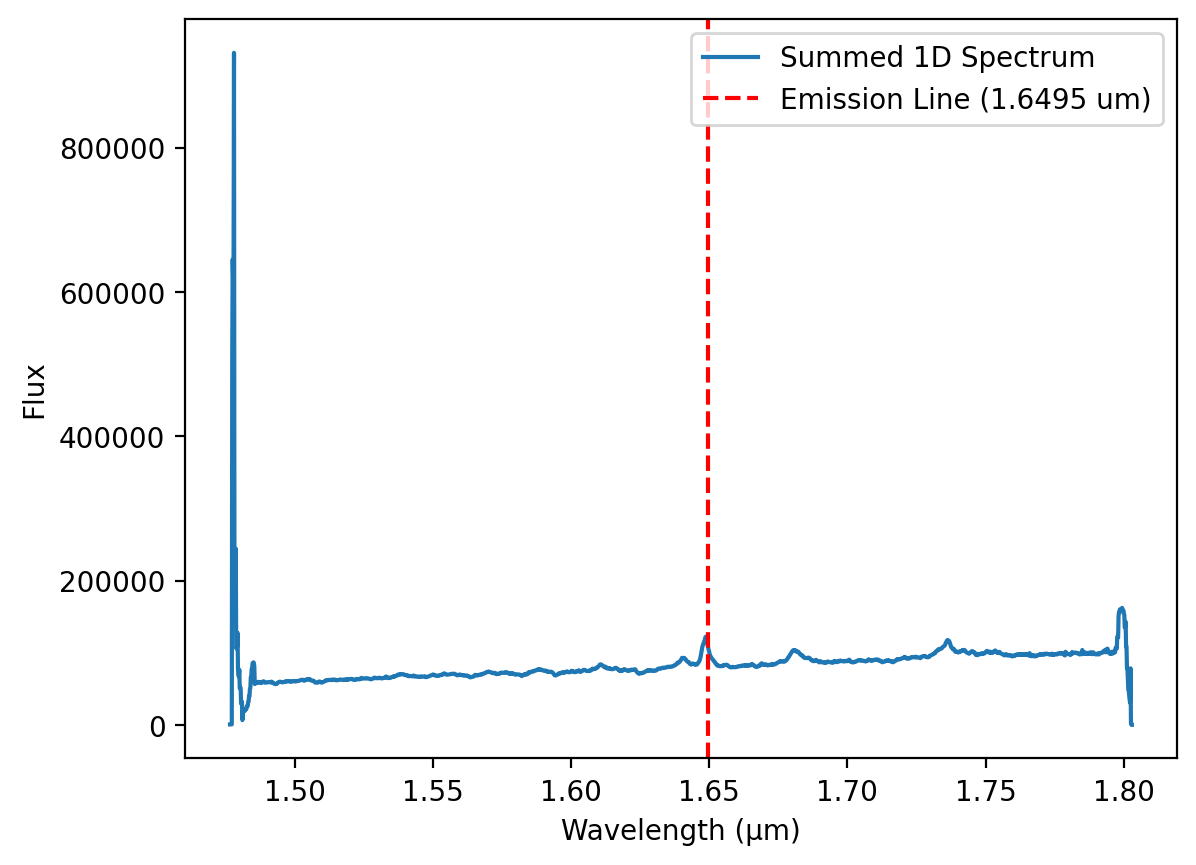
plt.plot(wave, flux1, label='Summed 1D Spectrum') # 绘制波长 vs. 总光谱
plt.axvline(emission_line, color='red', linestyle='--', label=f'Emission Line ({emission_line:.4f} um)') # 标出发射线位置
plt.xlabel('Wavelength (µm)') # x 轴标签:波长(微米)
plt.ylabel('Flux') # y 轴标签:光通量
plt.legend() # 显示图例
plt.show() # 显示图像
我们观察到,累加后的 1D 光谱在光谱两端表现出明显的噪声波动(“ratty”)。这一 1D 光谱数据数组超出了仪器的标称可用数据范围。因此,我们将忽略这些质量较差的光谱区域,并专注于活动星系核(AGN, Active Galactic Nucleus)的光通量分析。
我们感兴趣的 [Fe II] 发射特征是一个位于 1.65 微米短波端的明亮而强烈的发射线。需要注意的是,H I Brackett 12 发射线位于 [Fe II] 线的蓝侧,对其造成一定的污染。
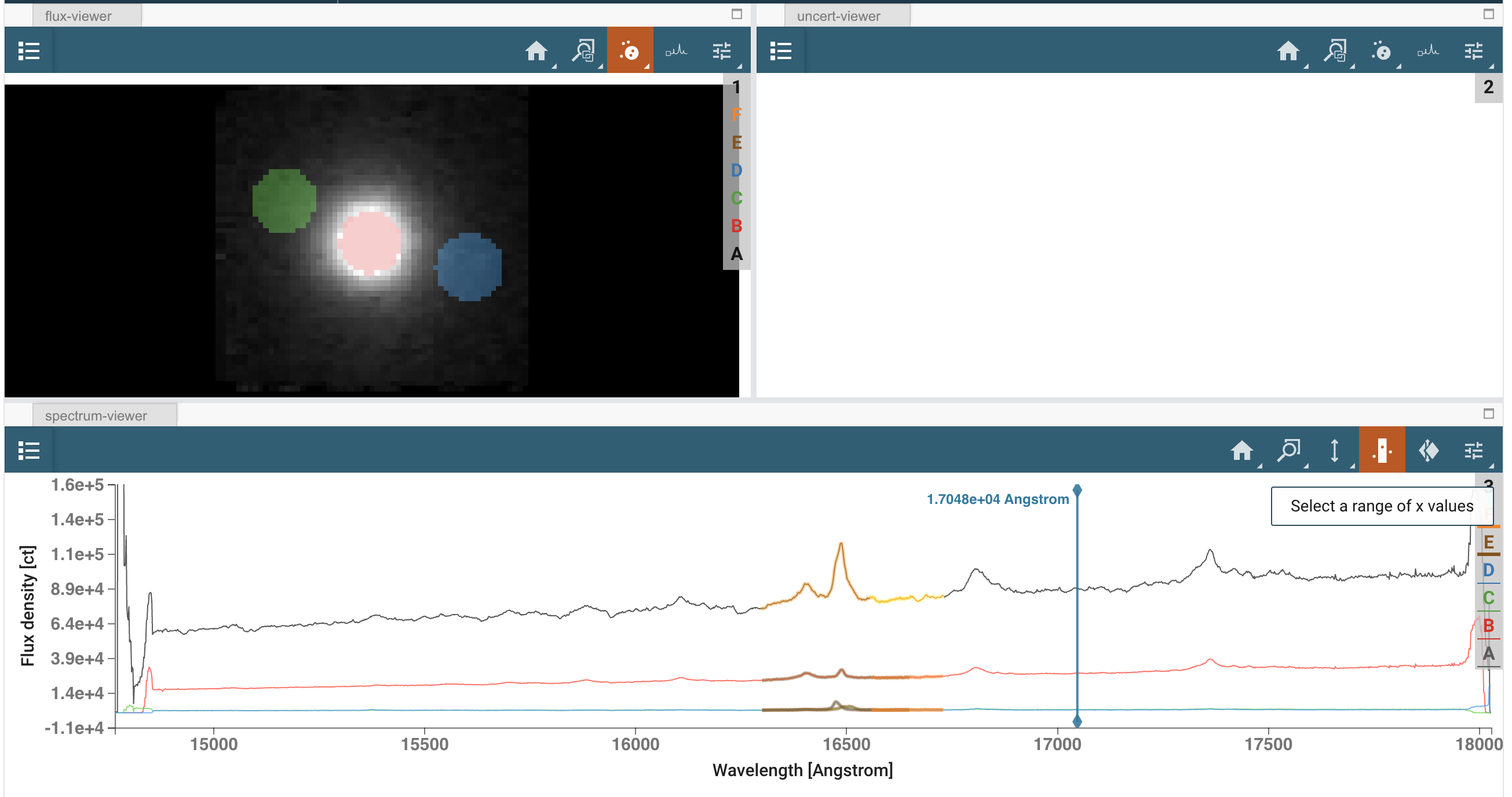
我们可以利用光谱图窗口来读取感兴趣的波长值,以便定义分析所需的光谱范围(可参考光谱图右下角的波长/光通量网格数据)。
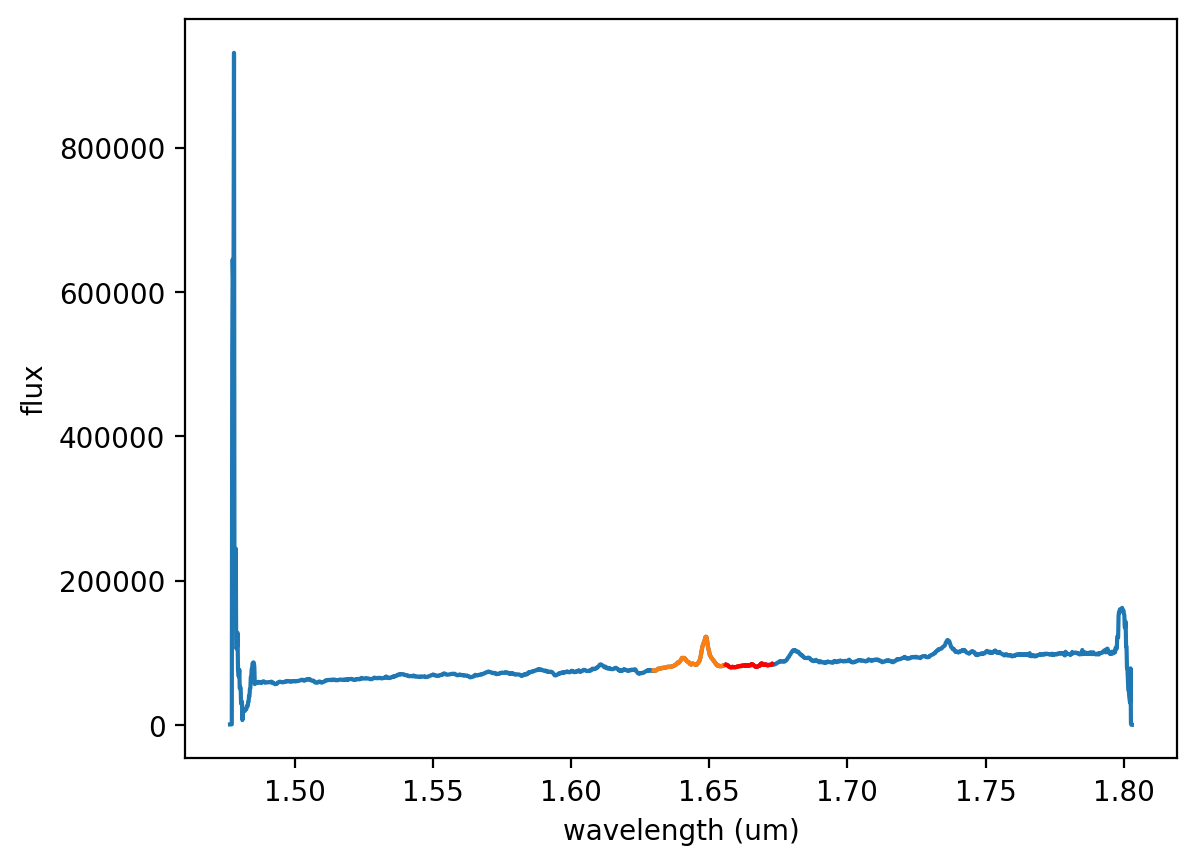
特别说明:在此数据集中,[Fe II] 发射线红侧(长波方向)的一部分光谱区域提供了一个较为干净的连续谱测量。然而,在 [Fe II] 和 H I Brackett 12 发射线的蓝侧(短波方向),存在其他的发射和吸收特征,使得明确识别连续谱变得非常困难。因此,相比于采用包含整个发射线的更大波长范围,在红侧区域进行简单的线性拟合会更加准确。
# 该单元定义了感兴趣的波长区域:围绕发射线的区域,以及
# 你想要非常准确地拟合和去除连续体的位置。绘制一个图,显示这些区域。
# 在这里我们选择一个包含发射线的区域
# 波长以及其周围的连续体的小范围。
# 通过调查上面图中的通量来确定这些限制。
# 从右下角的图信息中读取波长值。
wave_emission_limit1 = 1.630 # 发射线下限波长
wave_emission_limit2 = 1.665 # 发射线上限波长
# 在这里我们定义一个光谱范围,在该范围内我们将使用
# 通量生成连续体模型。该
# AGN在红移发射线附近的通量形状相当线性,因此我们将仅使用
# 发射特征红侧的短段光谱。
# 我们再次通过调查上面图窗口中的波长来确定这些值。
continuum_limit1 = 1.656 # 连续体下限波长
continuum_limit2 = 1.673 # 连续体上限波长
# 定义发射线周围的波长区域 - 索引
wavemin = (np.abs(wave - wave_emission_limit1)).argmin() # 找到发射线下限的索引
wavemax = (np.abs(wave - wave_emission_limit2)).argmin() # 找到发射线上限的索引
# 定义用于拟合连续体通量水平的波长区域 - 索引
continuummin = (np.abs(wave - continuum_limit1)).argmin() # 找到连续体下限的索引
continuummax = (np.abs(wave - continuum_limit2)).argmin() # 找到连续体上限的索引
# 显示用于发射线和连续体拟合的区域。如果看起来不合适,请更改上面的波长。
plt.figure(1) # 创建新的图形
plt.plot(wave, flux1) # 绘制整个光谱
plt.plot(wave[wavemin:wavemax], flux1[wavemin:wavemax]) # 绘制发射线区域
plt.plot(wave[continuummin:continuummax], flux1[continuummin:continuummax], color='r') # 绘制连续体区域,红色
plt.xlabel('wavelength (um)') # 设置x轴标签
plt.ylabel('flux') # 设置y轴标签
plt.show() # 显示图形
Cubeviz 可视化#
您还可以使用 Cubeviz 在 Jupyter Notebook 中可视化图像。
视频:#
此Cubeviz演示来自官方JWST观察者YouTube频道。它展示了如何使用Cubeviz进行特定科学案例的示例(并非本笔记本中的科学案例)。
vid = YouTubeVideo("ayb6OkmZUwU") # 创建一个YouTubeVideo对象,传入视频ID
display(vid) # 显示该YouTube视频
# 导入Cubeviz类
cubeviz = Cubeviz() # 创建Cubeviz实例
# 显示Cubeviz界面
cubeviz.show() # 调用show方法以显示界面
# 在这里,我们将数据加载到Cubeviz应用程序中。
with warnings.catch_warnings(): # 捕获警告
warnings.simplefilter('ignore') # 忽略警告
cubeviz.load_data(fn) # 加载数据文件fn到Cubeviz
下面的视频展示了该过程。以下步骤适用:
当您加载立方体时,您将在底部的光谱查看器中看到所有spaxels的合并光谱。
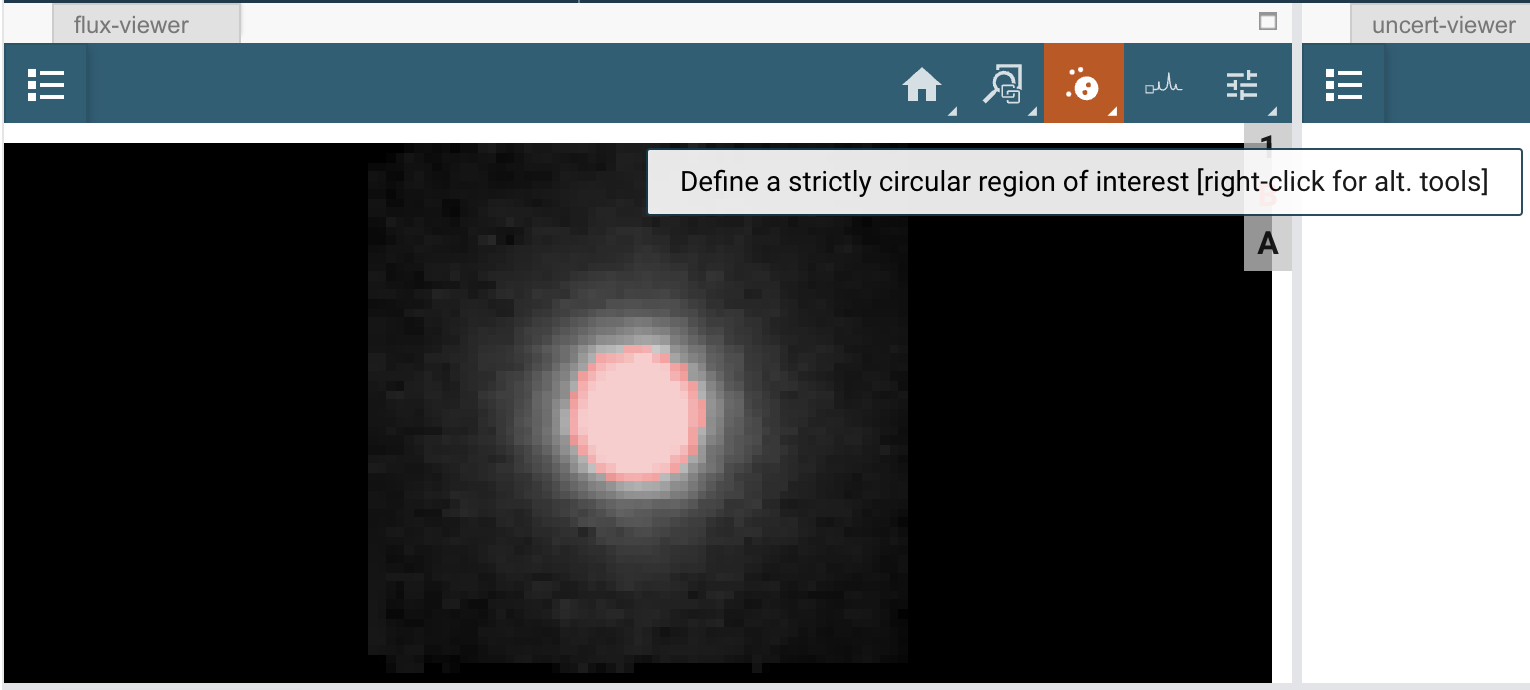
如果您在通量查看器中绘制一个区域(圆形或方形),您也会在光谱查看器中看到该特定区域的合并光谱。在这个例子中,我们首先要在明亮的活动星系核(AGN)通量的中心位置定义一个圆形区域,该位置大约位于立方体的中心。
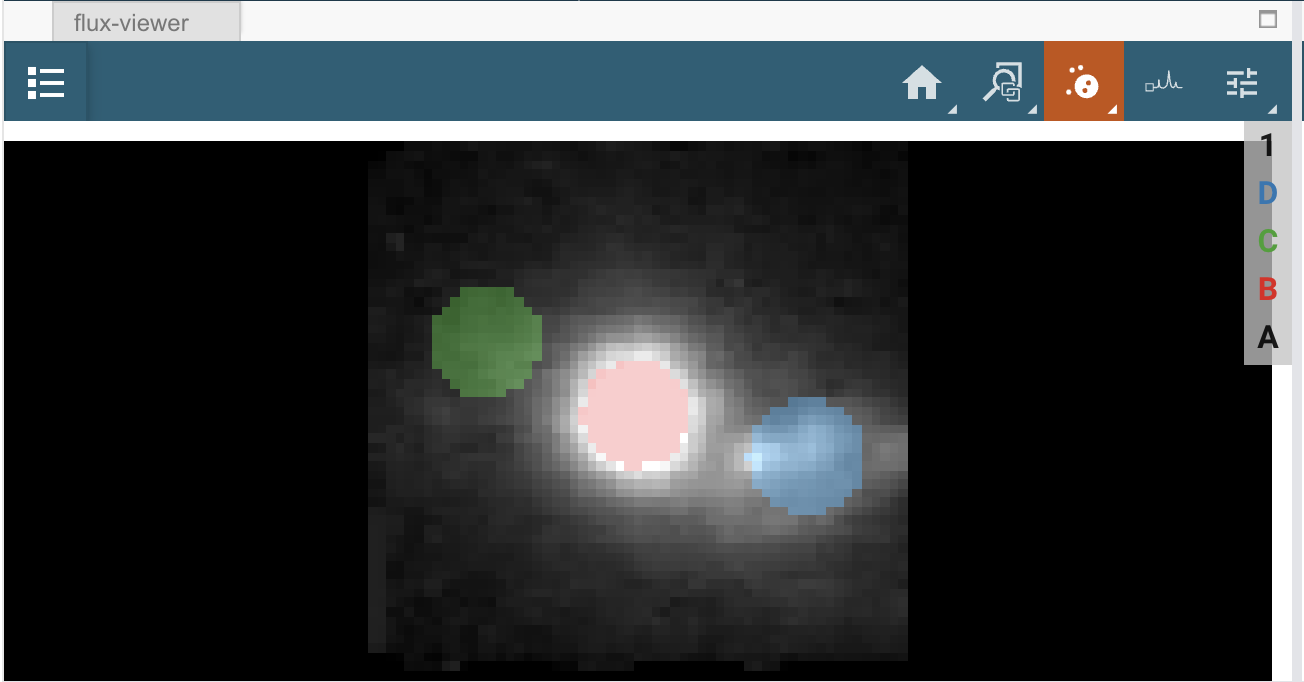
现在,使用通量查看器,再次使用“定义感兴趣的圆形区域”图标,在与[Fe II]的喷流发射相关的两个位置制作光谱。红移喷流大约位于x位置 = 12,y位置 = 36。这将是“子集2”,在显示中将以绿色显示。蓝移喷流大约位于像素索引单位的x位置 = 48,y位置 = 24。这将是“子集3”,在显示中将以蓝色显示。提示:光标的坐标在工具的顶部报告
定义你的光谱区域#
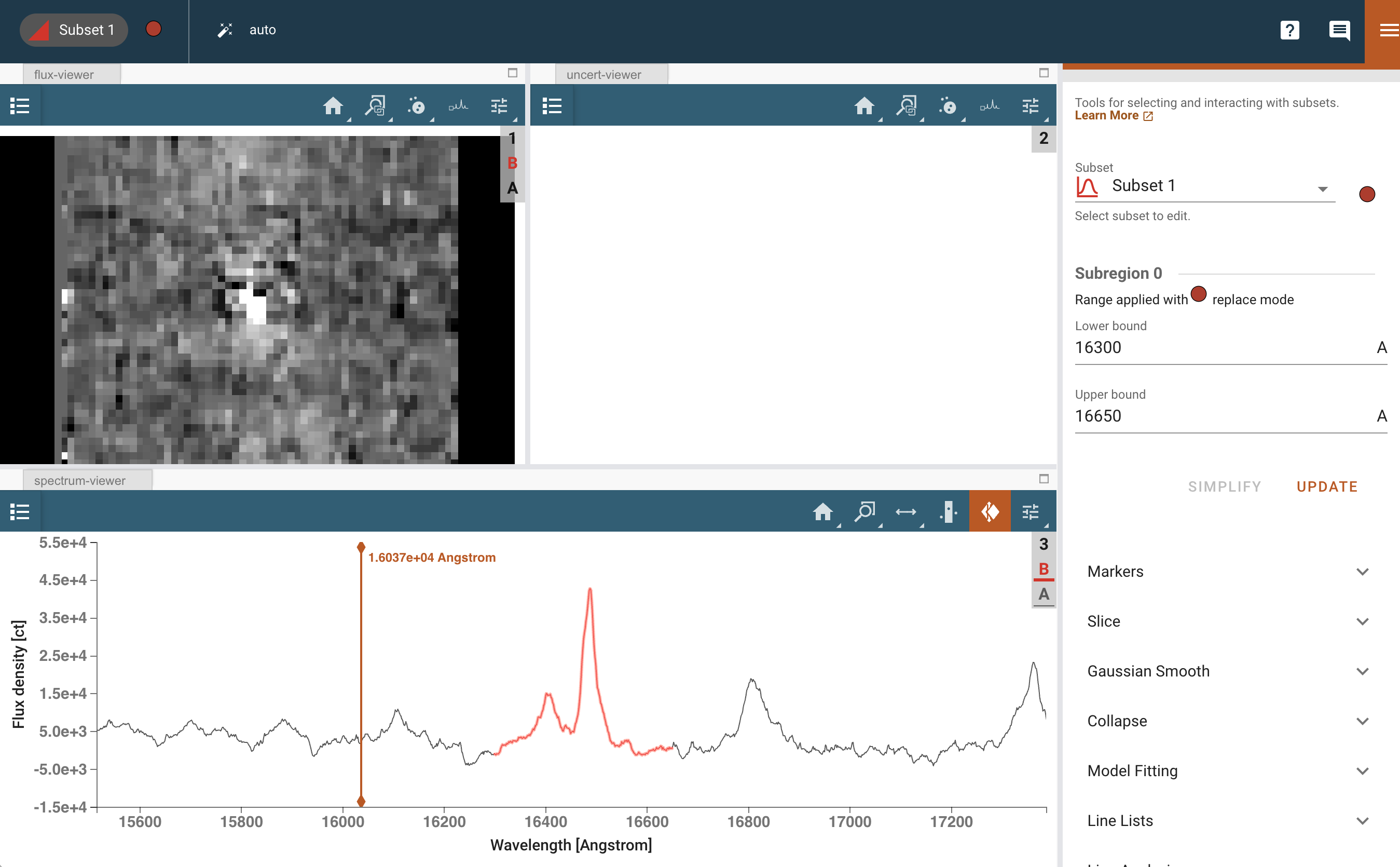
接下来,你需要在光谱查看器中定义你感兴趣的波长,以便进行线和连续谱分析。为此,你同样需要点击光谱查看器中的“定义感兴趣区域”图标,并拖动一个框覆盖你所需的波长。线发射(’Subset 4’)应大致覆盖1.630 - 1.665微米,而连续发射(’Subset 5’)应大致覆盖1.656 - 1.673微米。
提示:子集可以在子集工具插件中进行修改
一些注意事项:#
如果您的单元窗口需要滚动才能查看cubeviz中的不同显示,您可以在笔记本的主菜单中切换滚动窗口:单元 -> 当前输出 -> 切换滚动
为了更好地可视化立方体,您可以在绘图选项插件中更改显示选项。
在Cubeviz光谱查看器中提取子集光谱#
从光谱查看器中检索用户定义区域的光谱,作为Spectrum1D对象。首先,我们通过API创建区域,以防笔记本未以交互方式运行。
# 创建空间区域
spatial_regions = cubeviz.get_interactive_regions() # 获取当前的交互区域
if 'Subset 1' not in spatial_regions.keys(): # 检查是否存在子集1
agn_region = CirclePixelRegion(center=PixCoord(x=29, y=29), radius=6) # 创建AGN区域,中心点为(29, 29),半径为6
cubeviz.load_regions(agn_region) # 加载AGN区域
if 'Subset 2' not in spatial_regions.keys(): # 检查是否存在子集2
redshifted_outflow = CirclePixelRegion(center=PixCoord(x=12, y=36), radius=6) # 创建红移外流区域,中心点为(12, 36),半径为6
cubeviz.load_regions(redshifted_outflow) # 加载红移外流区域
if 'Subset 3' not in spatial_regions.keys(): # 检查是否存在子集3
blueshifted_outflow = CirclePixelRegion(center=PixCoord(x=48, y=24), radius=6) # 创建蓝移外流区域,中心点为(48, 24),半径为6
cubeviz.load_regions(blueshifted_outflow) # 加载蓝移外流区域
spatial_regions = cubeviz.get_interactive_regions() # 再次获取当前的交互区域
spatial_regions # 返回当前的空间区域
默认情况下,光谱是使用 sum 函数和光谱提取插件中的默认选项提取的。为了本笔记本的目的,我们希望使用 mean 函数提取光谱。我们可以通过界面进行操作,如下方截图所示,或者运行以下单元格。
spec_ext = cubeviz.plugins['Spectral Extraction'] # 获取光谱提取插件
spec_ext.function = 'Mean' # 设置提取函数为均值
spec_ext.aperture = 'Subset 1' # 设置光圈为子集1
spec_ext.add_results = 'Spectrum (Subset 1, mean)' # 添加结果标签
spec_ext.extract() # 执行提取操作
spec_ext.aperture = 'Subset 2' # 设置光圈为子集2
spec_ext.add_results = 'Spectrum (Subset 2, mean)' # 添加结果标签
spec_ext.extract() # 执行提取操作
spec_ext.aperture = 'Subset 3' # 设置光圈为子集3
spec_ext.add_results = 'Spectrum (Subset 3, mean)' # 添加结果标签
spec_ext.extract() # 执行提取操作
# 从cubeviz中提取与彩色区域对应的光谱
spectrum1 = cubeviz.get_data("Spectrum (Subset 1, mean)") # 获取AGN中心的光谱
spectrum2 = cubeviz.get_data("Spectrum (Subset 2, mean)") # 获取红移分量的光谱
spectrum3 = cubeviz.get_data("Spectrum (Subset 3, mean)") # 获取蓝移分量的光谱
spectrum1 # 显示AGN中心的光谱
# 提取在光谱查看器中定义的线区域
regions = cubeviz.specviz.get_spectral_regions() # 获取当前光谱区域
if "Subset 4" in regions.keys(): # 检查是否存在名为"Subset 4"的区域
line_region = regions["Subset 4"] # 如果存在,获取该区域
else: # 如果不存在
line_region = SpectralRegion(1.630*u.um, 1.665*u.um) # 创建一个新的光谱区域,范围为1.630到1.665微米
sv = cubeviz.app.get_viewer('spectrum-viewer') # 获取光谱查看器
sv.toolbar_active_subset.selected = [] # 清空当前活动子集的选择
sv.apply_roi(XRangeROI(16300, 16650)) # 应用一个新的感兴趣区域,范围为16300到16650
# 提取在光谱查看器中定义的连续区域
if "Subset 5" in regions.keys(): # 检查是否存在名为"Subset 5"的区域
continuum_region = regions["Subset 5"] # 如果存在,获取该区域
else: # 如果不存在
continuum_region = SpectralRegion(1.656*u.um, 1.673*u.um) # 定义一个新的连续区域
sv = cubeviz.app.get_viewer('spectrum-viewer') # 获取光谱查看器
sv.toolbar_active_subset.selected = [] # 清空当前活动子集的选择
sv.apply_roi(XRangeROI(16560, 16730)) # 应用一个新的感兴趣区域(ROI)
regions = cubeviz.specviz.get_spectral_regions() # 获取当前的光谱区域
regions # 返回光谱区域
# 应用光谱区域
# (如果用户没有在jdaviz中创建新的折叠光谱,则创建新的折叠光谱)
if not spectrum1: # 检查spectrum1是否存在
# 计算AGN的光通量,选择中心区域的像素进行求和
flux_agn = np.sum(cube[:, (ny//2)-3:(ny//2)+3, (nx//2)-3:(nx//2)+3], axis=(1, 2))
# 创建一个新的Spectrum1D对象,包含计算得到的光通量和波长
tmpspec = Spectrum1D(flux=flux_agn*u.Unit('count'), spectral_axis=wave*u.micron)
# 从临时光谱中提取线区域
spec_agn = extract_region(tmpspec, line_region)
# 从临时光谱中提取连续区域
spec_agn_continuum = extract_region(tmpspec, continuum_region)
else: # 如果spectrum1存在
# 从spectrum1中提取线区域
spec_agn = extract_region(spectrum1, line_region)
# 从spectrum1中提取连续区域
spec_agn_continuum = extract_region(spectrum1, continuum_region)
if not spectrum2: # 检查spectrum2是否存在
# 计算红光FeII的光通量,选择特定像素区域进行求和
flux_feii_red = np.sum(cube[:, (36)-3:(36)+3, (12)-3:(12)+3], axis=(1, 2))
# 创建一个新的Spectrum1D对象,包含计算得到的光通量和波长
tmpspec = Spectrum1D(flux=flux_feii_red*u.Unit('count'), spectral_axis=wave*u.micron)
# 从临时光谱中提取线区域
spec_feii_red = extract_region(tmpspec, line_region)
# 从临时光谱中提取连续区域
spec_feii_red_continuum = extract_region(tmpspec, continuum_region)
else: # 如果spectrum2存在
# 从spectrum2中提取线区域
spec_feii_red = extract_region(spectrum2, line_region)
# 从spectrum2中提取连续区域
spec_feii_red_continuum = extract_region(spectrum2, continuum_region)
if not spectrum3: # 检查spectrum3是否存在
# 计算蓝光FeII的光通量,选择特定像素区域进行求和
flux_feii_blue = np.sum(cube[:, (28)-3:(28)+3, (50)-3:(50)+3], axis=(1, 2))
# 创建一个新的Spectrum1D对象,包含计算得到的光通量和波长
tmpspec = Spectrum1D(flux=flux_feii_blue*u.Unit('count'), spectral_axis=wave*u.micron)
# 从临时光谱中提取线区域
spec_feii_blue = extract_region(tmpspec, line_region)
# 从临时光谱中提取连续区域
spec_feii_blue_continuum = extract_region(tmpspec, continuum_region)
else: # 如果spectrum3存在
# 从spectrum3中提取线区域
spec_feii_blue = extract_region(spectrum3, line_region)
# 从spectrum3中提取连续区域
spec_feii_blue_continuum = extract_region(spectrum3, continuum_region)
# 可视化新的子集
plt.figure() # 创建一个新的图形
plt.plot(spec_agn.spectral_axis, spec_agn.flux, color='black') # 绘制光谱轴与通量的关系,颜色为黑色
plt.title('Spectrum subset 1') # 设置图形标题
plt.xlabel('wavelength') # 设置x轴标签为波长
plt.ylabel('flux') # 设置y轴标签为通量
# 可视化新的子集
plt.figure() # 创建一个新的图形
plt.plot(spec_feii_blue.spectral_axis, spec_feii_blue.flux, color='b') # 绘制蓝色Fe II谱线
plt.plot(spec_feii_red.spectral_axis, spec_feii_red.flux, color='r') # 绘制红色Fe II谱线
plt.title('Spectra subset 2 and 3') # 设置图形标题
plt.xlabel('wavelength') # 设置x轴标签为波长
plt.ylabel('flux') # 设置y轴标签为通量
在光谱区域位置拟合连续谱#
打开模型拟合插件。这里有多个字段需要填写和下拉菜单供选择。重要的是要记住,数据菜单将仅提供可用于建模的光谱,而光谱区域菜单将仅提供可供选择的光谱区域子集。换句话说,您可以在特定的光谱区域内拟合光谱。如果未选择光谱区域,则整个波长数组将由该模式拟合。
我们将首先拟合一个单独的光谱,以测试我们的拟合参数是否合适,然后我们将切换到拟合整个立方体。
单个光谱
选择数据:光谱子集 1(均值)
选择光谱区域:子集 5
模型:Linear1D(线性一维)
ModelID(模型ID):L
点击“添加组件”
模型参数:保持默认
模型方程编辑器:L
模型标签:LinFitCont
点击“拟合模型”,这将拟合压缩后的光谱。
在光谱查看器中查看拟合结果,并确认您对此满意。
整个立方体
在顶部切换“立方体拟合”。
将名称更改为 LinFitCont_cube,然后再次点击“拟合模型”。
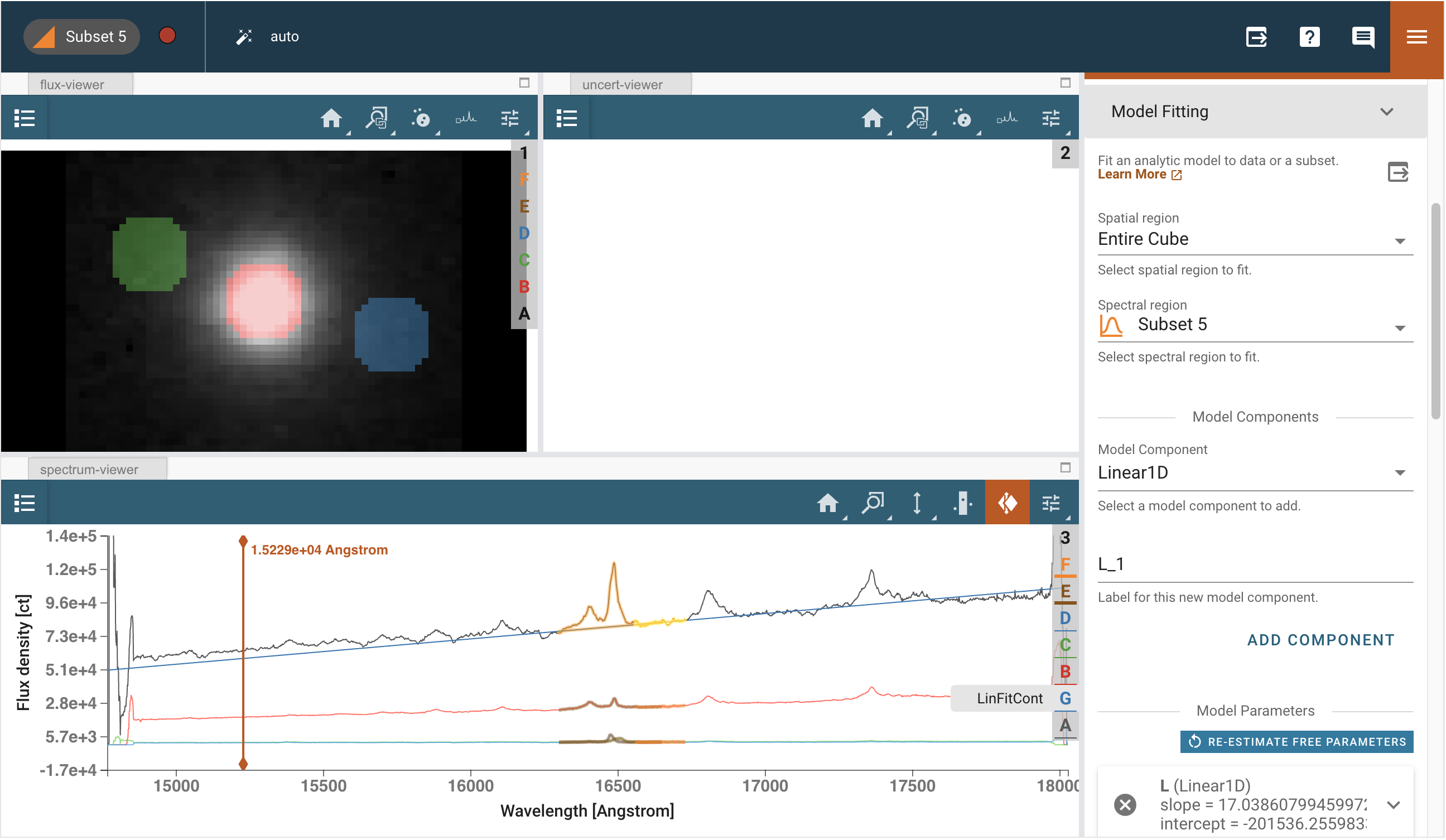
拟合后的立方体可以在2D查看器的数据下拉菜单中访问。
使用API替代#
models = cubeviz.get_models() # 获取当前模型
if 'LinFitCont' in models.keys(): # 检查是否存在线性拟合模型
singlemodel = models['LinFitCont'] # 如果存在,获取该模型
else:
# 打开模型拟合插件
plugin_mf = cubeviz.plugins['Model Fitting'] # 获取模型拟合插件
plugin_mf.open_in_tray() # 在插件托盘中打开
# 输入适当的数据集
plugin_mf.dataset = 'Spectrum (sum)' # 设置数据集为总光谱
plugin_mf.spectral_subset = 'Subset 5' # 设置光谱子集为子集5
# 输入模型组件
plugin_mf.create_model_component(model_component='Linear1D', # 创建线性一维模型组件
model_component_label='L1') # 设置模型组件标签为L1
# 模型方程会自动填充
plugin_mf.equation = 'L1' # 设置模型方程为L1
# 运行后,我们去GUI检查拟合是否合理
plugin_mf.add_results.label = 'LinFitCont' # 设置结果标签为LinFitCont
plugin_mf.cube_fit = False # 设置为非立方体拟合
plugin_mf.calculate_fit() # 计算拟合
if 'LinFitCont_cube (30, 30)' in models.keys(): # 检查是否存在立方体线性拟合模型
cubemodel = models['LinFitCont_cube'] # 如果存在,获取该模型
else:
# 打开模型拟合插件
plugin_mf = cubeviz.plugins['Model Fitting'] # 获取模型拟合插件
plugin_mf.open_in_tray() # 在插件托盘中打开
# 设置拟合为立方体
plugin_mf.cube_fit = True # 设置为立方体拟合
# 输入适当的数据集
plugin_mf.dataset = 'contents[SCI]' # 设置数据集为科学数据内容
plugin_mf.spectral_subset = 'Subset 5' # 设置光谱子集为子集5
# 输入模型组件
plugin_mf.create_model_component(model_component='Linear1D', # 创建线性一维模型组件
model_component_label='L2') # 设置模型组件标签为L2
# 模型方程会自动填充
plugin_mf.equation = 'L2' # 设置模型方程为L2
# 运行后,我们去GUI检查拟合是否合理
plugin_mf.add_results.label = 'LinFitCont_cube' # 设置结果标签为LinFitCont_cube
plugin_mf.calculate_fit() # 计算拟合
models = cubeviz.get_models() # 获取模型数据
# models # 注释掉的代码,可能用于调试或查看模型
models['LinFitCont_cube (30, 30)'] # 访问特定的线性拟合模型
拉取其他数据#
请注意,在 cubeviz 中,您可以通过使用 function 关键字参数(可选地)结合 spatial_subset 来返回如上所述的合并光谱,或者通过省略这些关键字来返回整个数据立方体,如下所示。
# 列出可用的数据
print(cubeviz.data_labels) # 打印数据标签
# 获取完整的原始数据立方体
scidata = cubeviz.get_data("contents[SCI]") # 从cubeviz中获取科学数据
scidata # 显示获取的数据
# 从Cubeviz中提取SCI立方体和连续模型,并制作连续减去的立方体
if 'LinFitCont_cube' in cubeviz.app.data_collection: # 检查数据集中是否包含'LinFitCont_cube'
cont_psf_cube = cubeviz.get_data("LinFitCont_cube") # 获取连续模型立方体
print('Check shape of the objects') # 打印检查对象的形状
print(scidata.shape) # 打印科学数据立方体的形状
print(cont_psf_cube.shape) # 打印连续模型立方体的形状
# 获取连续减去的立方体
sci_contsub = scidata - cont_psf_cube # 从科学数据中减去连续模型
# 保存到文件
# sci_contsub.write('NGC4151_Hband_ContinuumSubtract.fits', format='wcs1d-fits', overwrite=True) # 保存连续减去的立方体到文件
# cont_psf_cube.write('NGC4151_Hband_ContinuumPSF.fits', format='wcs1d-fits', overwrite=True) # 保存连续模型立方体到文件
开发者备注:
如果我尝试将立方体保存到文件中,会出现回溯错误,因为它们没有正确的头文件。
# 在Cubeviz中查看去除连续谱的立方体数据
if sci_contsub: # 检查是否存在去除连续谱的数据
with warnings.catch_warnings(): # 捕获警告
warnings.simplefilter('ignore') # 忽略警告
cubeviz2 = Cubeviz() # 创建Cubeviz实例
cubeviz2.load_data(sci_contsub, data_label='Continuum Subtracted') # 加载去除连续谱的数据,并设置标签
cubeviz2.show() # 显示Cubeviz窗口
使用numpy进行连续体减法的替代方法#
# 重新读取原始的IFU立方体以进行处理
cube_file = 'https://data.science.stsci.edu/redirect/JWST/jwst-data_analysis_tools/IFU_cube_continuum_fit/NGC4151_Hband.fits' # 定义立方体文件的URL
newfn = download_file(cube_file, cache=True) # 下载文件并缓存
newheader_cube = fits.getheader(cube_file) # 获取立方体文件的头信息
start_time = time.time() # 记录开始时间
sci_contsub_np = np.zeros([nx, ny, nz]) # 初始化科学数据的连续体减去数组
cont_psf_cube_np = np.zeros([nx, ny, nz]) # 初始化连续体PSF立方体数组
# 遍历立方体的每个像素
for i in range(1, nx-2): # 遍历x轴
for j in range(1, ny-2): # 遍历y轴
flux1 = cube[:, j, i] # 获取当前像素的光谱数据
cont_fit = np.polyfit(wave[continuummin:continuummax], flux1[continuummin:continuummax], 1) # 拟合连续体
fitval = np.poly1d(cont_fit) # 创建多项式对象
continuum = fitval(wave) # 计算连续体
sci_contsub_np[i, j, :] = flux1 - continuum # 进行连续体减法
cont_psf_cube_np[i, j, :] = continuum # 保存连续体PSF
print(sci_contsub_np.shape) # 打印科学数据的形状
del newheader_cube['MODE'] # 删除头信息中的'MODE'条目
# 将减去连续体后的立方体和PSF立方体写入新的FITS文件
fits.writeto('NGC4151_Hband_ContinuumSubtract_numpy.fits', sci_contsub_np, newheader_cube, overwrite=True) # 保存减去连续体后的立方体
fits.writeto('NGC4151_Hband_ContinuumPSF_numpy.fits', cont_psf_cube_np, newheader_cube, overwrite=True) # 保存连续体PSF立方体
print('Continuum subtracted cube saved. PSF continuum cube saved.') # 打印保存成功信息
开发者备注:
新创建的文件无法在Cubeviz中打开
拟合您的多组分高斯模型#
现在我们想要研究对 Br 12 发射特征的初步拟合,这是一个在波长上与我们的目标 [Fe II] 发射相邻的麻烦污染物。Br 12 是集中紧凑的,仅来自活动星系核(AGN)的核,而不是来自喷流。绘制拟合结果的图。
首先,按照顶部执行的类似程序选择感兴趣的波长区域。没有选项可以设置用户输入的光谱区域,因此我们建议放大并用眼睛绘制。线发射(“子集 1”)应再次大致覆盖 1.630 - 1.665 微米。
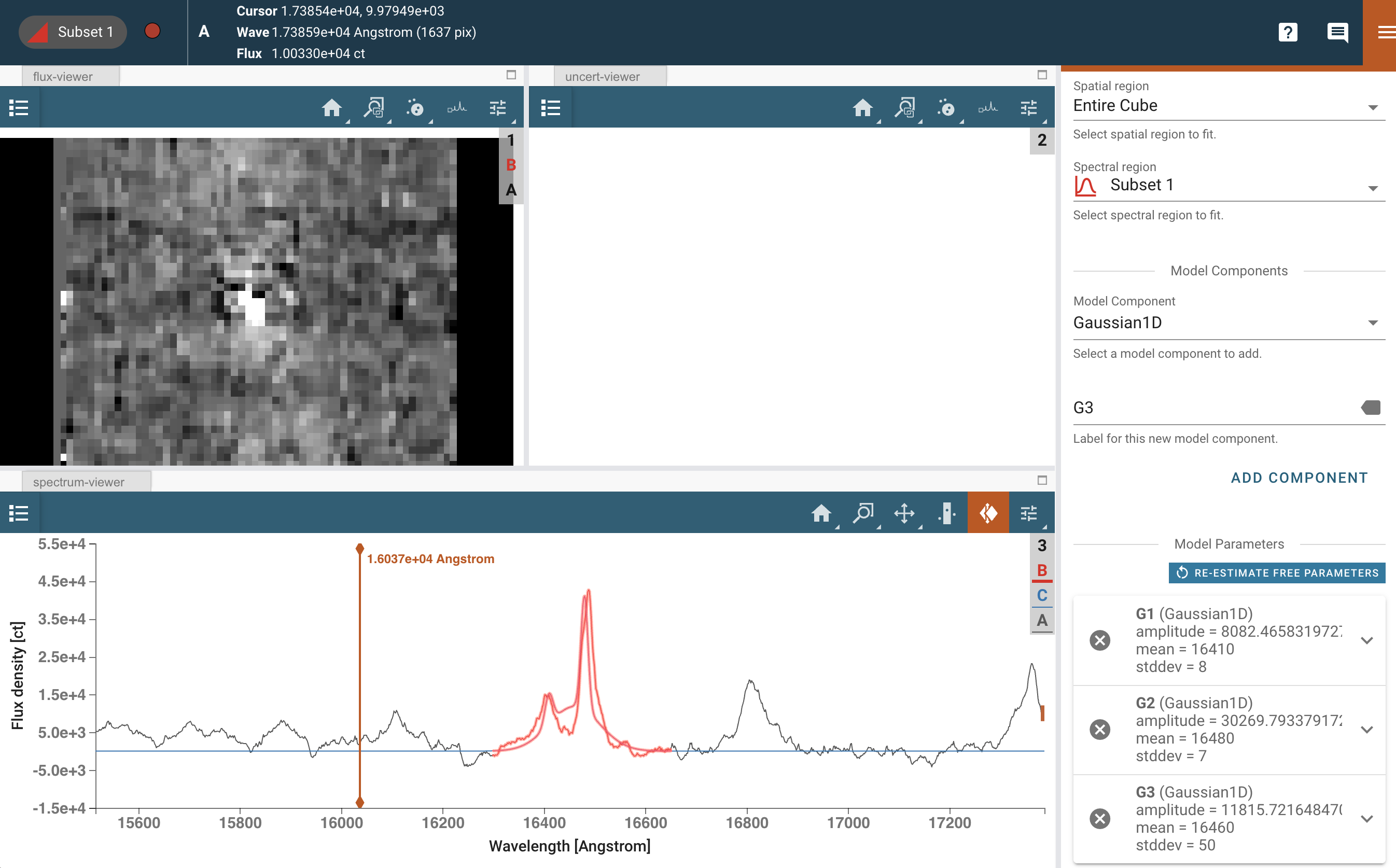
对于这个例子,我们建议设置一个 3 组分的高斯模型,输入如下:
打开模型拟合插件。有许多字段需要填写和下拉菜单可供选择。重要的是要记住,数据菜单将仅提供要建模的光谱,而光谱区域菜单将仅提供可选择的光谱区域子集。换句话说,您可以在特定的光谱区域中拟合光谱。如果未选择光谱区域,则整个波长数组将由模型进行拟合。
数据:光谱(总和)
光谱区域:子集 1
模型:三个不同的高斯,ModelID 设置为 G1、G2 和 G3
模型参数:
G1:标准差=8,均值=16410
G2:标准差=7,均值=16480
G3:标准差=50,均值=16460
如果需要,您可以启用“固定”选项,但这些数字应该为拟合提供一个良好的起始猜测。
模型方程编辑器:G1+G2+G3
模型标签:GaussAll
点击拟合,这将拟合压缩光谱。
在光谱查看器中查看拟合结果,并确认您对此感到满意。如有必要,请进行修改。
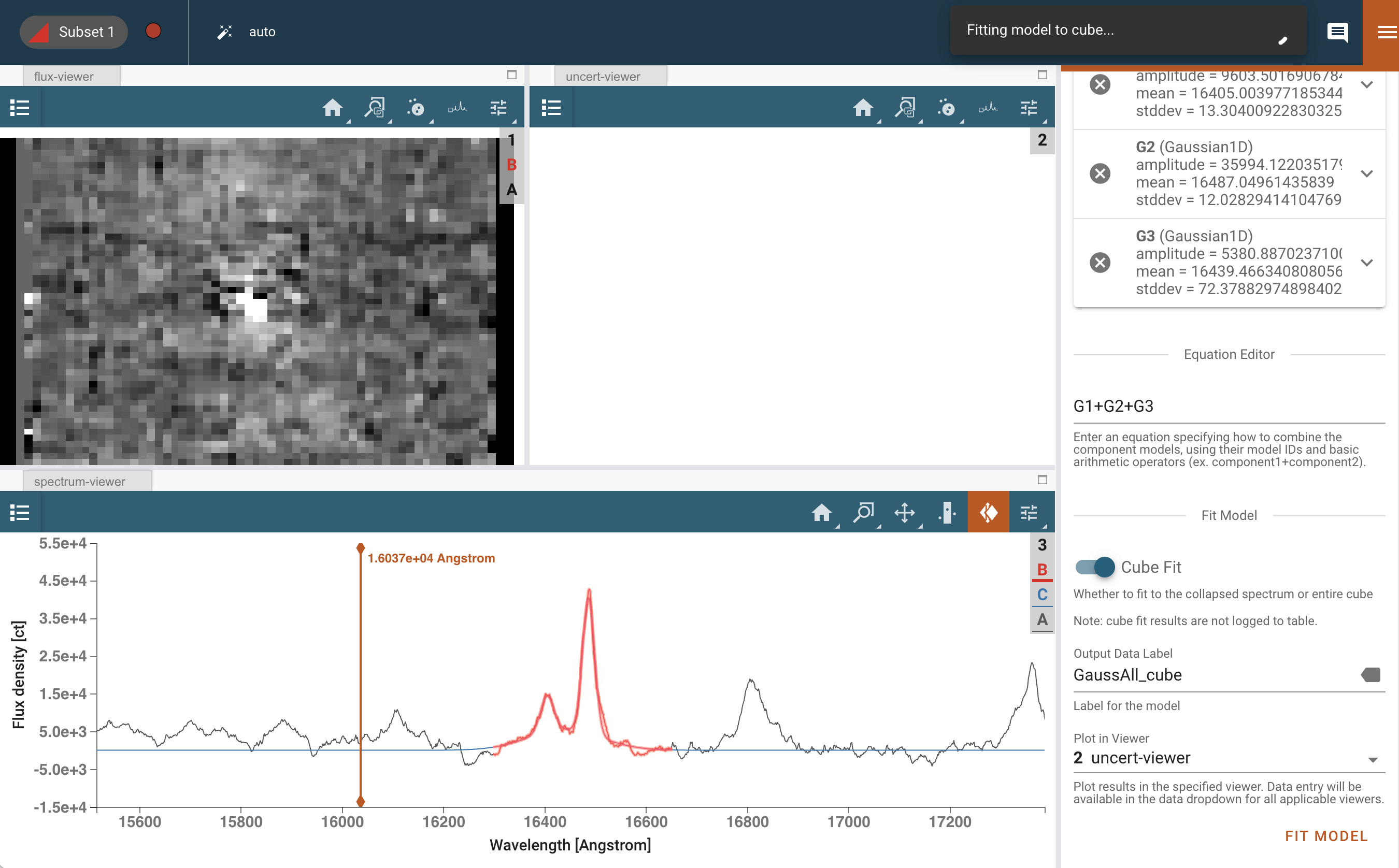
然后移除“固定”选项,切换到立方体拟合,将名称更改为 GaussAll_cube,并再次运行。
这将再次创建两个模型,现在可以在数据下拉菜单中访问:
对压缩立方体中线的 1D 线性拟合。
对立方体中每个像素的线的 3D 线性拟合。
哇,那个多组分拟合看起来很棒。真不错。
现在我们将使用前一个单元中的连续体点扩散函数(continuum psf)立方体,结合上面单元中创建的布拉凯特模型(Brackett model),来创建一个完整的三维模型,表示不受流出物[Fe II]影响的中心发射。
开发者备注:
对整个数据立方体的拟合会卡住,永远无法结束
练习#
现在你可以尝试调整上面的代码,以通过 API 运行模型拟合!
提示:
plugin_mf.create_model_component(model_component='Gaussian1D', model_component_label='G1')
plugin_mf.set_model_component('G1', 'mean', value=16410)
请提供您希望我添加中文注释的代码,我将根据您的要求进行处理。
从Cubeviz中提取我们需要的内容#
# 提取在光谱查看器中定义的光谱区域
regions = cubeviz2.specviz.get_spectral_regions() # 从specviz获取光谱区域
print(regions) # 打印获取的光谱区域
# 检查"Subset 1"是否在光谱区域的键中
if "Subset 1" in regions.keys():
line_region = regions["Subset 1"] # 如果存在,获取"Subset 1"对应的光谱区域
else:
line_region = SpectralRegion(1.630*u.um, 1.665*u.um) # 如果不存在,定义一个新的光谱区域
# 列出可用的数据
alldata = cubeviz2.app.data_collection # 获取数据集合
print(alldata) # 打印数据集合
print() # 打印空行以便于阅读
# 列出在光谱查看器中可用的光谱
spec = cubeviz2.specviz.get_spectra() # 获取可用的光谱
print(spec) # 打印光谱信息
开发者说明:目前无法在创建的模型立方体上使用光谱提取插件。如果需要“均值”模型,则应在提取的“均值”光谱上计算1D模型。
# 获取高斯模型光谱和模型立方体
spec_ext2 = cubeviz2.plugins['Spectral Extraction'] # 获取光谱提取插件
spec_ext2.function = 'Mean' # 设置提取函数为均值
spec_ext2.aperture = 'Entire Cube' # 设置提取区域为整个立方体
spec_ext2.add_results = 'Spectrum entire (mean)' # 添加结果名称为“整个光谱(均值)”
spec_ext2.extract() # 执行光谱提取
# 这仅用于后续模型的光谱轴
all_spec = cubeviz2.get_data('Spectrum entire (mean)') # 获取整个光谱(均值)数据
if 'GaussAll' in alldata: # 检查数据中是否存在'GaussAll'
gauss_spec = cubeviz2.get_data('GaussAll') # 获取AGN中心模型光谱。这是“总和”,而不是“均值”
print('Model spectrum 1D available') # 打印模型光谱1D可用信息
print(gauss_spec) # 打印高斯光谱
else:
gauss_spec = False # 如果不存在,则设置高斯光谱为False
print('No GaussAll model created') # 打印未创建GaussAll模型的信息
print() # 打印空行
if 'GaussAll_cube' in alldata: # 检查数据中是否存在'GaussAll_cube'
gauss_cube = cubeviz2.get_data('GaussAll_cube') # 获取AGN中心模型立方体
params = cubeviz2.get_model_parameters() # 获取模型参数
print('Model spectrum 3D available') # 打印模型光谱3D可用信息
else:
gauss_cube = False # 如果不存在,则设置高斯立方体为False
params = False # 设置参数为False
print('No GaussAll_cube model created') # 打印未创建GaussAll_cube模型的信息
print() # 打印空行
# 检查用户是否使用了Cubeviz(如上所示),如果没有,则读取预制数据
if gauss_cube is False: # 如果高斯立方体为False
# 获取未使用Cubeviz创建的模型立方体和连续立方体
fn = download_file('https://data.science.stsci.edu/redirect/JWST/jwst-data_analysis_tools/IFU_cube_continuum_fit/gauss_model_cube.fits', cache=False) # 下载高斯模型立方体
tgauss_cube = fits.getdata(fn) # 获取高斯立方体数据
gauss_cube = tgauss_cube.transpose(2, 1, 0) # 转置立方体数据
print('Shape of downloaded model cube: ', gauss_cube.shape) # 打印下载的模型立方体形状
fn_continuum = 'NGC4151_Hband_ContinuumPSF_numpy.fits' # 设置连续立方体文件名
continuum_cube = fits.open(fn_continuum, memmap=False) # 打开连续立方体文件
newfull_header = fits.getheader(fn_continuum) # 获取文件头信息
continuum_data = continuum_cube[0].data # 获取连续数据
print('Shape of downloaded continuum cube: ', continuum_data.shape) # 打印下载的连续立方体形状
else:
print('Shape of created model cube: ', gauss_cube.shape) # 打印创建的模型立方体形状
continuum_data = sci # 在Cubeviz1中创建的连续数据
print('Shape of created continuum cube: ', continuum_data.shape) # 打印创建的连续立方体形状
print() # 打印空行
if params is False: # 如果参数为False
fn = download_file('https://data.science.stsci.edu/redirect/JWST/jwst-data_analysis_tools/IFU_cube_continuum_fit/gauss_params.pkl', cache=True) # 下载高斯参数文件
params = load_obj(fn) # 加载参数对象
print('Keys of downloaded model parameters: ', params.keys()) # 打印下载的模型参数的键
else:
print('Keys of created model parameters: ', params.keys()) # 打印创建的模型参数的键
print() # 打印空行
if not all_spec: # 如果all_spec为False
fn = download_file('https://data.science.stsci.edu/redirect/JWST/jwst-data_analysis_tools/IFU_cube_continuum_fit/all_spec.fits', cache=False) # 下载所有光谱文件
all_spec = Spectrum1D.read(fn) # 读取光谱数据
print('Shape of downloaded continuum subtracted spectrum: ', all_spec.shape) # 打印下载的去除连续光谱的形状
else:
print('Shape of created continuum subtracted spectrum: ', all_spec.shape) # 打印创建的去除连续光谱的形状
print() # 打印空行
if gauss_spec is False: # 如果高斯光谱为False
fn = download_file('https://data.science.stsci.edu/redirect/JWST/jwst-data_analysis_tools/IFU_cube_continuum_fit/gauss_spec.fits', cache=False) # 下载高斯光谱文件
gauss_spec = Spectrum1D.read(fn) # 读取高斯光谱数据
print('Shape of downloaded model spectrum: ', gauss_spec.shape) # 打印下载的模型光谱形状
else:
print('Shape of created model spectrum: ', gauss_spec.shape) # 打印创建的模型光谱形状
# 用仅包含两个感兴趣成分的高斯模型覆盖原有模型
if 'GaussAll_cube' in alldata: # 检查数据中是否包含'GaussAll_cube'
gauss_cube_2component = gauss_cube.flux * 0. # 初始化一个与gauss_cube相同形状的零数组
model_label = "GaussAll_cube" # 设置模型标签为'GaussAll_cube'
specunit = 1. # 设置光谱单位为1(无单位)
ampunit = 1. # 设置幅度单位为1(无单位)
else: # 如果'GaussAll_cube'不在数据中
gauss_cube_2component = gauss_cube * 0. # 初始化一个与gauss_cube相同形状的零数组
model_label = "GaussAll_3d" # 设置模型标签为'GaussAll_3d'
specunit = u.Angstrom # 设置光谱单位为埃(Angstrom)
ampunit = u.Unit('count') # 设置幅度单位为计数(count)
print(gauss_cube_2component.shape) # 打印gauss_cube_2component的形状
nx, ny, nz = gauss_cube_2component.shape # 获取gauss_cube_2component的维度
for i in range(0, nx-1): # 遍历第一个维度(x轴)
for j in range(0, ny-1): # 遍历第二个维度(y轴)
amp1 = params[model_label]['amplitude_0'][i][j] # 获取第一个高斯成分的幅度
amp2 = params[model_label]['amplitude_2'][i][j] # 获取第二个高斯成分的幅度
m1 = params[model_label]['mean_0'][i][j]*1E10 # 获取第一个高斯成分的均值并转换为米
m2 = params[model_label]['mean_2'][i][j]*1E10 # 获取第二个高斯成分的均值并转换为米
stdev1 = params[model_label]['stddev_0'][i][j]*1E10 # 获取第一个高斯成分的标准差并转换为米
stdev2 = params[model_label]['stddev_2'][i][j]*1E10 # 获取第二个高斯成分的标准差并转换为米
g1 = Gaussian1D(amplitude=amp1*ampunit, mean=m1*specunit, stddev=stdev1*specunit) # 创建第一个高斯模型
g2 = Gaussian1D(amplitude=amp2*ampunit, mean=m2*specunit, stddev=stdev2*specunit) # 创建第二个高斯模型
gauss_cube_2component[i, j, :] = g1(all_spec.spectral_axis) + g2(all_spec.spectral_axis) # 计算两个高斯模型的和并存储
gauss_cube_2component_spec = Spectrum1D(spectral_axis=all_spec.spectral_axis, # 创建Spectrum1D对象
flux=gauss_cube_2component * ampunit) # 设置光谱轴和通量
注意: 为什么不一次性对所有成分进行拟合,而是在这里添加连续体成分?
# 将连续体立方体添加到新的模型立方体中
full_model = gauss_cube_2component_spec + continuum_data # 将两个立方体相加,生成完整模型
print(full_model.shape) # 打印完整模型的形状
# 从模型中减去以创建最终立方体,其中[Fe II]发射被孤立。
# 重新读取原始IFU立方体以进行操作
cube_file = 'https://data.science.stsci.edu/redirect/JWST/jwst-data_analysis_tools/IFU_cube_continuum_fit/NGC4151_Hband.fits' # 定义立方体文件的URL
newfinalsub_header = fits.getheader(cube_file) # 获取立方体文件的头信息
# 从cubeviz中获取的立方体是scidata
final_sub_cube = scidata.flux.value - full_model.flux.value # 从scidata中减去模型的flux值以得到最终立方体
final_sub_cube_units = Spectrum1D(spectral_axis=scidata.spectral_axis, # 创建一个Spectrum1D对象,包含光谱轴和减去模型后的flux值
flux=final_sub_cube*ampunit) # 将减去模型后的flux值乘以单位以获得最终flux
print(final_sub_cube_units.shape) # 打印最终立方体的形状
print(scidata.shape) # 打印原始scidata的形状
import os # 导入os模块,用于与操作系统交互
# 删除当前目录中任何现有的输出文件
if os.path.exists("NGC4151_Hband_FinalSubtract.fits"): # 检查文件是否存在
os.remove("NGC4151_Hband_FinalSubtract.fits") # 如果存在,删除该文件
else:
print("The file does not exist") # 如果不存在,打印提示信息
if os.path.exists("NGC4151_Hband_ContinuumandBrackettModel.fits"): # 检查另一个文件是否存在
os.remove("NGC4151_Hband_ContinuumandBrackettModel.fits") # 如果存在,删除该文件
else:
print("The file does not exist") # 如果不存在,打印提示信息
开发者注释: Fits writeto 出现错误。暂时将单元格设为原始格式。
# 制作最终图表以展示原始光谱、模型拟合和最终的连续体+高斯减去的立方体
plt.figure() # 创建一个新的图形窗口
plt.xlim([16200, 16650]) # 设置x轴范围
plt.ylim([600, 900]) # 设置y轴范围
plt.plot(all_spec.spectral_axis, continuum_data[30, 30, :], label='Continuum') # 绘制连续体数据
plt.plot(all_spec.spectral_axis, scidata.flux[30, 30, :], label='Original Data') # 绘制原始数据
plt.plot(all_spec.spectral_axis, full_model.flux[30, 30, :], label='2 Component Model') # 绘制2成分模型数据
plt.plot(all_spec.spectral_axis, final_sub_cube_units.flux[30, 30, :]+700*ampunit, label='Model Subtraction+Offset') # 绘制模型减去后的数据并加上偏移量
plt.legend() # 显示图例
plt.xlabel('wavelength') # 设置x轴标签为“波长”
plt.ylabel('flux') # 设置y轴标签为“通量”
plt.show() # 显示图形